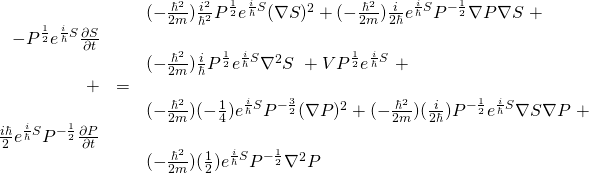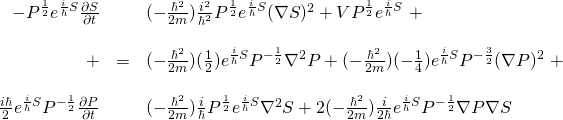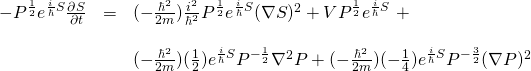Contents
- Introduction
- Requisite mathematics
- Primer on quantum mechanics
- Schrodinger equation
- Derivation of Bohm’s equations
- Significance of Bohm’s equations
- Bohmian mechanics answers to questions raised by the Copenhagen interpretation
- Conclusion
Introduction
Quantum mechanics is arguably the most successful theory in the history of science. Its predictions have been extensively borne out by empirical evidence and its tenets have never been contradicted by experiment. Yet despite its utility in predicting the results of experiments, many of its formalisms – especially those that constitute the standard or Copenhagen interpretation of quantum mechanics – are counterintuitive, and to this day, are the subject of intense controversy and debate.
A major source of contention is what’s called the measurement problem. Basically, in the standard interpretation of quantum mechanics, any property of a particle is indeterminate – indeterminate, that is, until the property is measured. For example, before the position of a particle is measured, its position is indeterminate; it could be anywhere. And granted, in practice, most of this probability is usually concentrated over a small area but there could be a chance that it could be found anywhere else in the universe. As will be discussed below, there is a thing called a wave function associated with each measurable property of a particle. It consists of probability amplitudes – a probability amplitude being associated with each possible measurement outcome. When that probability amplitude is squared, one obtains the probability that the given measurement will occur. The wave function rolls along in time deterministically. Until it is measured, that is. Then suddenly, the probability of the property taking on the value of the measurement becomes 100% and the probability of it being any other value becomes 0%. This is called wave function collapse. The question to many is: why should the wave function behave in one manner during measurement and in another manner at all other times.
Another phenomenon that has a nonintuitive explanation in the standard interpretation of quantum mechanics is the double slit experiment. Take a source of photons and shoot them at a detector screen. Between the source and the detector screen is a barrier with 2 slits in it. Cover 1 slit and shoot photons at the detector. If they hit the detector they turn the black detector white. What is the result? The photons make a white band on the detector behind the slit that’s open – behaving as if they were particles. Cover that slit and open the other. The photons again make a white band on the detector behind the slit that’s open. Now open both slits and shine the source. The photons make bands of white alternating with black – a pattern called an interference pattern; a pattern that would result if light photons were waves that went through both slits at the same time interfering with themselves, the peaks of each wave interfering constructively with other peaks and the valleys interfering destructively. Now repeat the above experiments but shoot the photons one at a time. What happens? The photons make a white spot on the detector one at a time, but after many photons have been delivered, the same patterns emerge as those that occurred when a stream of photons were administered. 2 questions arise: 1) How can the photons behave like particles in one instance (when only one slit is open) and like a wave in another circumstance (i.e., when both slits are open)? and 2) How can photons shot one at a time “figure out” where to land when they create the interference pattern when both slits are open? Some have speculated that the act of measurement somehow determines the behavior of the photons. That is, if an observer knows which slit the photons are going through (i.e., as in the case of only 1 slit open), then the photons have a definite location (i.e., behind the open slit). However, if the observer doesn’t know which slit the photon is going through, then it “goes through both slits” – a kind of superposition of states like that described for particle location – resulting in the interference pattern. Ultimately, the explanation of these results according to the standard interpretation of quantum mechanics is: that’s just the way it is; measurement and observation do, in fact, constitute “special” circumstances. This is unsettling to some physicists.
It gets worse. What if we open both slits but put a device between slit A and the detector which can tell us whether or not a photon goes through slit A. When we shine light toward the detector, we get 2 bands, one behind each slit; the interference pattern disappears. Did the measurement process cause this? The Copenhagen interpretation of quantum physics might not go so far as to invoke causation. But it does say that this is just the way it is. Which implies, again, that there is something special about the act of measurement.
But it gets even more bizarre. Take the same setup as the last example but randomly activate or leave inactive the device behind slit A after photons of light (or other particles) have passed the device on their way to the detector. If the device is activated after the particle has passed it, then there is no interference pattern. If the device is not activated after the particle has passed it, then there is an interference pattern. According to the standard interpretation of quantum mechanics, this is just the way it is; again, the measurement process (in this case, the device behind slit A) effects the behavior of the particles (albeit in a strange way – after the photons should have “made their decision” whether to behave as particles or waves). This is just a general description of this class of experiments. A detailed description of the most compelling of these experiments, the delayed quantum eraser experiment, can be found here.
Finally, there’s entanglement. This quantum phenomenon can be seen with various types of particles but we’ll examine the behavior of entangled photons here.
To understand photon entanglement, we first need to discuss a property of photons called polarization. Basically, this refers to the direction in which a photon’s electric field is oscillating. Polarization filters are devices that allow photons that are polarized in the given direction to which the filter is set to pass through while blocking photons that are polarized in a direction ![]() from the direction to which the filter is set. Suppose that a group of photons all polarized at
from the direction to which the filter is set. Suppose that a group of photons all polarized at ![]() are shot at a filter set at
are shot at a filter set at ![]() . All will pass through the filter. Said another way, if a single photon polarized at
. All will pass through the filter. Said another way, if a single photon polarized at ![]() is fired at a filter set at
is fired at a filter set at ![]() , there is a 100% chance that it will pass through the filter. On the other hand, if photons polarized at
, there is a 100% chance that it will pass through the filter. On the other hand, if photons polarized at ![]() are shot at a filter set at
are shot at a filter set at ![]() , none of them will get through. But what if photons polarized at
, none of them will get through. But what if photons polarized at ![]() are fired at a filter set at
are fired at a filter set at ![]() ? Half get through and half don’t. The explanation, according to the standard interpretation of quantum mechanics, is that the photon is in a superposition of polarization states, half polarized in the
? Half get through and half don’t. The explanation, according to the standard interpretation of quantum mechanics, is that the photon is in a superposition of polarization states, half polarized in the ![]() direction and half in the
direction and half in the ![]() direction. Each individual photon may or may not get through (and we can’t predict which result will occur for any individual photon). What we do know, however, is that there is a 50% probability of each photon passing through the filter. Thus, if we send in a large number of photons, we get the observed result.
direction. Each individual photon may or may not get through (and we can’t predict which result will occur for any individual photon). What we do know, however, is that there is a 50% probability of each photon passing through the filter. Thus, if we send in a large number of photons, we get the observed result.
Now about entanglement. It’s not important for this discussion how it happens, but take it on faith that pairs of photons can be produced that are polarized both either in the same direction or in antiparallel directions. For our purposes here, let’s consider entangled pairs polarized in the same direction. Keep one partner for each pair here on earth and send the other off to, say, Alpha Centauri. If we measure the polarization of each photon with filters set at the same angles, the photon pair either both go through their respective filter or both do not. This is not surprising; a program of how to behave could have been communicated to the photons at the time of their creation. But what if, at each site, we measure at 1 of 3 angles selected randomly. If the photon pairs were programmed to behave in specific ways with each angle of measurement (i.e., there were local hidden variables at play), then a certain percentage of measurements would agree at both sites; specifically, they would follow an inequality called Bell’s Inequality. If, on the other hand, the photons behave quantum mechanically with superposition of states until measured, then a different percentage of measurements would be found (i.e., Bell’s inequality would be violated). A detailed discussion of Bell’s inequality can be found elsewhere on this site by clicking on the following link:
https://www.samartigliere.com/physics/quantum-mechanics/
Bell published a paper about his inequality in 1964. However, it took until 1982 to develop adequate technology to put Bell’s inequality to the test. In that year, Alain Aspect published a paper describing experimental evidence that supported quantum theory instead of a classical local hidden variables theory.
Again, central to the standard quantum mechanics interpretation of this phenomenon are the concepts of superposition and quantum indeterminacy.
Eminent theoretical physicist David Bohm originally wrote a textbook on quantum mechanics that was based on this standard (or Copenhagen) interpretation. Not all of the experimental evidence described above was available to Bohm at the time but the general ideas of indeterminacy were certainly present. But these concepts must have been troubling to Bohm because, in 1952, he published 2 papers outlining a theory in which particles possess a definite spatial position and trajectory at all times but still reproduce the results of quantum mechanical experiments. This theory is now commonly referred to as Bohmian mechanics and it is the first of these papers – the one that derives the basic equations of Bohmian mechanics – that will be examined in the remainder of this article.
Requisite mathematics
Understanding Bohmian mechanics requires considerable background in mathematics. Accordingly, I’ve put together some information on mathematics that might be useful. It is by no means exhaustive, but instead, attempts to review topics that are pertinent to the derivation of Bohmian mechanics. At the same time, in some respects, it is more detailed than necessary, in anticipation of expanding it in the future. A link to my page on background mathematics is
Primer on quantum mechanics
Not only does the derivation of the equations of Bohmian mechanics require background in mathematics, it also requires some knowledge of quantum mechanics. For this reason, I have developed a primer on quantum mechanics. Similar to the page on mathematics, coverage of the subject is far from complete, yet in some areas, is probably a bit over-detailed, again, in anticipation of a future more comprehensive quantum mechanics page. Hopefully, though, it will provide enough information to make the discussion on Bohmian mechanics on this page understandable. Here is a link to this quantum mechanics article:
Schrodinger equation
There are many who consider the Schrodinger equation one of the most important equations in quantum mechanics. It is also key to the development of Bohmian mechanics. Thus, we begin this discussion of Bohmian mechanics with a derivation of this equation.
It is well known that individual results of quantum mechanics experiments cannot be definitively predicted, but instead, only the probability of individual results of an experiment can be predicted. However, quantum states are essentially a list of probability amplitudes for events that determine the probabilities for individual results of an experiment. And it turns out that the time evolution of these quantum states is actually deterministic. Furthermore, if two states start out the same, they will remain the same in the future, and if start out the same, they will always remain the same. Such time evolution of a quantum system is called unitary evolution.
Consider a quantum system. We’ll represent the state of this system at some time, ![]() , by a state vector
, by a state vector ![]() . Similarly, we’ll represent the initial state of the system by the state vector
. Similarly, we’ll represent the initial state of the system by the state vector ![]() . To get from
. To get from ![]() to
to ![]() ,
, ![]() must be acted upon by an operator,
must be acted upon by an operator, ![]() , that causes a unitary evolution to
, that causes a unitary evolution to ![]() . This process is expressed mathematically by the following equation:
. This process is expressed mathematically by the following equation:
(1) ![]()
Before going any further, let’s take a closer look at ![]() .
.
First, if ![]() transforms one quantum state into another, it must be a linear operator. For a definition of linear operator, click here.
transforms one quantum state into another, it must be a linear operator. For a definition of linear operator, click here.
Second, it must create unitary evolution of the quantum states upon which it operates. As suggested above, if two systems are distinct at ![]() , they will always be distinct. In quantum mechanics, an example of distinct states are orthogonal states (i.e., states whose inner product is 0):
, they will always be distinct. In quantum mechanics, an example of distinct states are orthogonal states (i.e., states whose inner product is 0):
(2) ![]()
And if there is unitary evolution, these states stay orthogonal at all subsequent times:
(3) ![]()
To see this, take the bra counterpart of equation 1:
(4) ![]()
If
![]()
then
(5) ![]()
Plug equation 4 and equation 5 into equation 3:
(6) ![]()
Since any time can be considered ![]() and any subsequent time can be considered time
and any subsequent time can be considered time ![]() , the above equation must hold at all times. The only way that this can be true is if
, the above equation must hold at all times. The only way that this can be true is if
(7) ![]()
The relationship described by equation 7 constitutes the definition of a unitary operator.
In physics, we often consider what happens to a system when an infinitesimal incremental change is made, then add up the effects of all of these changes to make a general statement. In this case, consider the change that occurs over an infinitesimal time interval, ![]() . We established above, that time evolution in quantum physics is unitary. That means that
. We established above, that time evolution in quantum physics is unitary. That means that
(8) ![]()
If we make a tiny change to ![]() by adding the effect of an operator,
by adding the effect of an operator, ![]() , over that tiny time interval,
, over that tiny time interval, ![]() , then we have
, then we have
(9) ![]()
The reason that we put an ![]() and a minus sign before
and a minus sign before ![]() is to make subsequent mathematical manipulations easier.
is to make subsequent mathematical manipulations easier.
The complex conjugate of equation 9 is
(10) ![]()
Plugging equations 9 and 10 into equation 8:
(11) ![]()
![]() is tiny to begin with. Therefore,
is tiny to begin with. Therefore, ![]() is negligible (e.g., if
is negligible (e.g., if ![]() , then
, then ![]() ). So the term
). So the term ![]() can be ignored. That gives us
can be ignored. That gives us
(12) ![]()
![]() . Subtract I^2 from both sides:
. Subtract I^2 from both sides:
(13) ![]()
Divide both sides by ![]() . That leaves
. That leaves
(14) ![]()
That means that ![]() is a hermitian operator. But
is a hermitian operator. But ![]() has additional significance: it is the quantum Hamiltonian, an analogue of the classical Hamiltonian which is a representation of the total energy of a system.
has additional significance: it is the quantum Hamiltonian, an analogue of the classical Hamiltonian which is a representation of the total energy of a system.
From equation 1, we can infer that
(15) ![]()
Next, from equation 9, substitute ![]() into equation 15 for
into equation 15 for ![]() . We get
. We get
(16) ![]()
Subtract ![]() from both sides:
from both sides:
![]()
Divide both sides by ![]() :
:
(17) ![]()
Now take the limit ![]() of both sides of equation 17 (note that there is no
of both sides of equation 17 (note that there is no ![]() on the right side of the equation so the right side of the equation is unaffected):
on the right side of the equation so the right side of the equation is unaffected):
(18) ![]()
But ![]() is the definition of the derivative of
is the definition of the derivative of ![]() ,
, ![]() . Therefore,
. Therefore,
(19) ![]()
Unfortunately, the units on the left side and right side of equation 19 don’t match. The units on the left side of the equation are ![]() . On the other hand, the units on the right side of the equation are that of the Hamiltonian which represents energy,
. On the other hand, the units on the right side of the equation are that of the Hamiltonian which represents energy, ![]() (think kinetic energy
(think kinetic energy ![]() with units
with units ![]() . The solution to this problem is to multiply the left side of the equation by a constant,
. The solution to this problem is to multiply the left side of the equation by a constant, ![]() which has units
which has units ![]() . When we multiply this by the units already present on the left side of equation 19,
. When we multiply this by the units already present on the left side of equation 19, ![]() , we get
, we get ![]() which is exactly what we have on the right side of the equation. Doing this, we obtain:
which is exactly what we have on the right side of the equation. Doing this, we obtain:
(20) ![]()
Finally, divide both sides of the equation by ![]() . We end up with
. We end up with
(21) ![]()
This is the generalized version of the famous time-dependent Schrodinger equation.
There is another version of the Schrodinger equation, the time-independent Schrodinger equation:
(22) ![]()
where
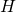 is the quantum Hamiltonian
is the quantum Hamiltonian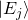 are state vectors that are eigenvectors of
are state vectors that are eigenvectors of 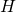
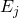 are the eigenvalues of
are the eigenvalues of 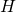 (which represent the possible values of energy that can be measured)
(which represent the possible values of energy that can be measured)
However, this version of the equation is not pertinent to our current discussion so we’ll leave explanation of it for another time. For now, what we want to do is derive the Schrodinger equation for a particle moving through a potential energy field since this is the system for which we will derive the equations of Bohmian mechanics.
We’ll start with the equation ![]() . We’ll drop the bra/ket notation,
. We’ll drop the bra/ket notation, ![]() since we’ll be dealing with continuous functions of position,
since we’ll be dealing with continuous functions of position, ![]() , and time,
, and time, ![]() . Thus, this equation becomes:
. Thus, this equation becomes:
![]()
Multiply both sides by ![]() :
:
![]()
As alluded to above, in Hamiltonian classical mechanics, the Hamiltonian, ![]() equals the total energy,
equals the total energy, ![]() , of the system under consideration which, for a particle moving through a potential field equals the kinetic energy,
, of the system under consideration which, for a particle moving through a potential field equals the kinetic energy, ![]() , plus the potential energy,
, plus the potential energy, ![]() . That is,
. That is,
![]()
But ![]() . However, in quantum mechanics, we need to use hermitian operators to multiply (i.e., operate on) state functions like
. However, in quantum mechanics, we need to use hermitian operators to multiply (i.e., operate on) state functions like ![]() . The momentum operator,
. The momentum operator, ![]() , in quantum mechanics is
, in quantum mechanics is
![]()
This formula may seem a bit puzzling at first, but an analysis of units shows that this makes perfect sense:
![]()
The ![]() in the expression for
in the expression for ![]() is to make
is to make ![]() Hermitian.
Hermitian.
So the classical expression ![]() , in quantum mechanics, becomes:
, in quantum mechanics, becomes:
![]()
The Hermitian operator for potential energy, ![]() is just
is just ![]() . Substituting these values into the Schrodinger equation, we get:
. Substituting these values into the Schrodinger equation, we get:
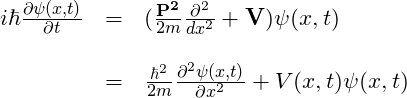
The equation above represents the evolution in time of a particle moving under the influence of a potential energy field in one dimension. To represent this scenario with the particle moving in three dimensions under the influence of a 3-dimensional potential energy field, we can make ![]() boldface. Thus, we have:
boldface. Thus, we have:
![]()
This isn’t quite how Schrodinger derived it but it’s it works and is simpler. To see a derivation more akin to how Schrodinger did it, check out the following link:
https://byjus.com/physics/derivation-of-schrodinger-wave-equation/
Derivation of Bohm’s equations
In the last section, we derived the iconic Schrodinger equation:
![]()
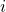 is the unit imaginary number and equals square root of -1 (
is the unit imaginary number and equals square root of -1 (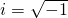 ).
).
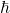 is the reduced Planck’s constant =
is the reduced Planck’s constant = 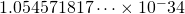
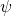 is the wave function, which is a complex function of spatial coordinates,
is the wave function, which is a complex function of spatial coordinates,  , and time,
, and time, 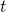 . Here
. Here  stands for all of the usual 3-dimensional spatial directions, which we frequently denote
stands for all of the usual 3-dimensional spatial directions, which we frequently denote 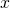 ,
, 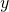 and
and  , not just the
, not just the 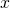 direction.
direction.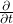 is the partial derivative – specifically of the wave function,
is the partial derivative – specifically of the wave function, 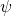 – with respect to time. It measures the change in the wave function with time.
– with respect to time. It measures the change in the wave function with time.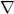 , called the nabla symbol, is a vector differential operator. It takes the derivative – in this case, of
, called the nabla symbol, is a vector differential operator. It takes the derivative – in this case, of 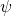 – with respect to each of the 3 dimensions of space. In plain language, it measures how the wave function,
– with respect to each of the 3 dimensions of space. In plain language, it measures how the wave function, 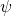 , varies with change of position, in all three spatial directions. Except, we have to apply this operator twice which means we’re evaluating the change of the change in position.
, varies with change of position, in all three spatial directions. Except, we have to apply this operator twice which means we’re evaluating the change of the change in position.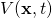 is a potential energy field which also varies with with time, at each position in space.
is a potential energy field which also varies with with time, at each position in space.
We said that the wave function, ![]() , varies with time, at each point in space. This can be expressed, mathematically, by this equation:
, varies with time, at each point in space. This can be expressed, mathematically, by this equation:
![]()
To see from where this equation originates, click here.
Let’s see what happens if we plug in ![]() for
for ![]() in the Schrödinger equation and see what happens. We start with:
in the Schrödinger equation and see what happens. We start with:
![]()
For the rest of this proof, we’ll leave out the ![]() to save space, recognizing that when we see
to save space, recognizing that when we see ![]() , we mean
, we mean ![]() , and when we see
, and when we see ![]() , we mean
, we mean ![]() .
.
With that said, we’ll calculate the above derivatives piece-by-piece. We’ll start with the left-hand sided of the equation.
To carry out this calculation, we need to apply the product rule and the chain rule. These rules are discussed and proven at the links below:
Here’s a quick review of these rules:
Product rule: ![]()
Chain rule: ![]()
In our case here, ![]() is analogous to
is analogous to ![]() and
and ![]() is analogous
is analogous ![]() . Therefore,
. Therefore,
By the product rule, ![]() .
.
And by the chain rule,
![]() (
(![]() is discussed here)
is discussed here)
![]() . Here’s why:
. Here’s why:
Let ![]() .
. ![]() .
. ![]() . Thus,
. Thus, ![]()
One more comment before we actually get into the proof. We us ![]() to represent the derivative when we’re dealing with only one variable. We use partial derivatives, (e.g.,
to represent the derivative when we’re dealing with only one variable. We use partial derivatives, (e.g., ![]() ), when we’re dealing with more than one variable in one expression. When taking the partial derivative with respect to a variable, we treat the other variables like constants. For example:
), when we’re dealing with more than one variable in one expression. When taking the partial derivative with respect to a variable, we treat the other variables like constants. For example:
![]()
Now onto our calculation of the terms of the left-hand side of the equation that we want to evaluate.
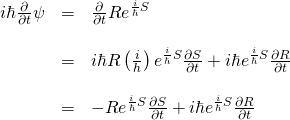
Now for the double partial derivative on the right side of the equation:
![Rendered by QuickLaTeX.com \begin{array}{rcl} -\frac{h^2}{2m}\nabla^2 \psi &=& \nabla^2 Re^{\frac{i}{\hbar}S}\\ &\,&\\ &=& -\frac{h^2}{2m}\left[\nabla \nabla \left(Re^{\frac{i}{\hbar}S}\right)\right]\\ &\,&\\ &=& -\frac{h^2}{2m}\left[\nabla \left( R(\frac{i}{\hbar})e^{\frac{i}{\hbar}S}\nabla S + e^{\frac{i}{\hbar}S}\nabla R \right)\right]\\ &\,&\\ &=&-\frac{h^2}{2m}\left[ \left( (\frac{i}{\hbar})R(\frac{i}{\hbar})e^{\frac{i}{\hbar}S}\nabla S + (\frac{i}{\hbar})e^{\frac{i}{\hbar}S}\nabla R \right)\nabla S + e^{\frac{i}{\hbar}S}\nabla^2 R + (\frac{i}{\hbar})Re^{\frac{i}{\hbar}S}\nabla^2 S + \nabla R (\frac{i}{\hbar}) e^{\frac{i}{\hbar}S}\nabla S \right]\\ &\,&\\ &=&\left( -\frac{h^2}{2m} (\frac{i^2}{\hbar^2})Re^{\frac{i}{\hbar}S}\nabla S -\frac{h^2}{2m} (\frac{i}{\hbar})e^{\frac{i}{\hbar}S}\nabla R \right)\nabla S -\frac{\hbar^2}{2m} e^{\frac{i}{\hbar}S}\nabla^2 R -\frac{\hbar^2}{2m} (\frac{i}{\hbar})Re^{\frac{i}{\hbar}S}\nabla^2 S -\frac{h^2}{2m} (\frac{i}{\hbar}) \nabla R e^{\frac{i}{\hbar}S}\nabla S \\ &\,&\\ &=&\frac{1}{2m}Re^{\frac{i}{\hbar}S}(\nabla S)^2 -\frac{i\hbar}{2m} e^{\frac{i}{\hbar}S}\nabla R \nabla S -\frac{h^2}{2m} e^{\frac{i}{\hbar}S}\nabla^2 R -\frac{i\hbar}{2m} Re^{\frac{i}{\hbar}S}\nabla^2 S -\frac{i\hbar}{2m} e^{\frac{i}{\hbar}S}\nabla R \nabla S \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-8330f22db43857bb4da8bad448e43d41_l3.png)
Now let’s put together the right-hand and left-hand sides of the Schrödinger equation into which we substituted for ![]() :
:
![]()
Since the terms on the right equal the terms on the left-hand side, we can separate the equations into two equations and we can arrange the terms on each side into any order we like as long as all are included. Here is how Bohm separated them:
![]()
Divide both sides by ![]() . We get:
. We get:
![]()
Here is the second equation:
![]()
We can reduce this equation by dividing through by ![]() :
:
![]()
We said that ![]() represents the amplitude of the wave function at each point in space, and that amplitude varies with time. According to quantum mechanical formalisms, the square of the wave function amplitude equals the probability of a particle being found at a specific location,
represents the amplitude of the wave function at each point in space, and that amplitude varies with time. According to quantum mechanical formalisms, the square of the wave function amplitude equals the probability of a particle being found at a specific location, ![]() , at a given time,
, at a given time, ![]() . We designate this probability
. We designate this probability ![]() . That means that
. That means that
![]() and
and ![]()
Next, we need to plug ![]() into the Schrödinger equation in place of
into the Schrödinger equation in place of ![]() and embark on a prolonged process of painful differential and algebraic manipulation similar to that which we just endured. If you’d like to see these calculations, click here:
and embark on a prolonged process of painful differential and algebraic manipulation similar to that which we just endured. If you’d like to see these calculations, click here:
If you didn’t click the button above, what we wind up with after going through all of these calculations is:
![]()
If we rearrange terms in the above equation, we obtain the equation that Bohm presented in his original paper:
(23) ![]()
Significance of Bohm’s equations
So what is the significance of this equation? It’s significance is its similarity to an equation called the Hamilton-Jacobi equation. In order to understand why this is important, we need to consider the meaning of the Hamilton-Jacobi equation.
Most non physicists who have had some exposure to physics have been exposed to Newtonian mechanics, the physics that is traditionally taught in high school and first year undergraduate physics courses. We won’t go into this subject here. An excellent treatment of this subject can be viewed, for free, online, at Khan Academy, at the following link:
https://www.khanacademy.org/science/physics
However, two of the most important equations in Newtonian mechanics are:
![]() where
where
![]() = force
= force
![]() = mass
= mass
![]() = acceleration
= acceleration
and
![]() where
where
![]() = force
= force
![]() = potential energy
= potential energy
![]() = the change in
= the change in ![]() which occurs with change in position,
which occurs with change in position, ![]()
These equations represent mathematical descriptions of a particle with a mass, ![]() , moving in one direction of space (which we’ll call
, moving in one direction of space (which we’ll call ![]() ) within a potential energy field,
) within a potential energy field, ![]() , (which varies according to its position along
, (which varies according to its position along ![]() ). A potential energy field is associated with a force and, in turn, cause the particle to accelerate (i.e., causes a change in its velocity per unit time). If there were no potential energy field then there would be no force acting on the particle and the particle would move along
). A potential energy field is associated with a force and, in turn, cause the particle to accelerate (i.e., causes a change in its velocity per unit time). If there were no potential energy field then there would be no force acting on the particle and the particle would move along ![]() with the same velocity forever. However, if there is potential energy present, then there is also an associated force and this force causes the particle to change its velocity.
with the same velocity forever. However, if there is potential energy present, then there is also an associated force and this force causes the particle to change its velocity.
It turns out that Newtonian mechanics does not provide the only description of this physical system. There are 3 other formulations of what is called classical mechanics (physics that don’t involve relativity or quantum theory). The 2 main ones are Lagrangian mechanics and Hamiltonian mechanics. In turn, the Hamilton-Jacobi equation is more or less a spinoff of the Lagrangian and Hamiltonian formulations. These alternative formulations provide various advantages over Newtonian mechanics in different situations. One of the advantages is that they provide insights about and links to advanced physics that are not so obvious from the equations of Newtonian mechanics. Still, Newtonian equations of motion can be derived from the other formulations and thus, the Newtonian and alternative formulations of classical physics are equivalent.
There are three other pages on this site which treat these alternative formulations in some detail. They can be found at the following links:
The reader is encouraged to view these pages. Otherwise, what follows is bound to make little sense.
At any rate, the bottom line is that the Hamilton-Jacobi equation provides a classical physics description of a particle moving in a potential energy field that is equivalent to Newtonian mechanics. Yet, at the same time, its form is very similar to the equation that Bohm derived from the Schrodinger equation, which is the quantum mechanical description of a particle moving in a potential energy field. What is the Hamilton-Jacobi equation? Here it is:
(24) ![]()
To understand what this equations means, we need to examine each term individually.
From the article on the Hamiltonian mechanics, we know that the Hamiltonian, ![]() , equals the total energy of a system which equals the kinetic energy (the energy of motion) and the potential energy of the system. The potential energy we’ve been talking about can be of several varieties – things like electrical potential energy and gravitational energy; potential energy related to the strong and weak nuclear forces. It stems from the configuration of a particle’s environment which determines the nature of the forces that act on the particle. The equation for the Hamiltonian is as follows:
, equals the total energy of a system which equals the kinetic energy (the energy of motion) and the potential energy of the system. The potential energy we’ve been talking about can be of several varieties – things like electrical potential energy and gravitational energy; potential energy related to the strong and weak nuclear forces. It stems from the configuration of a particle’s environment which determines the nature of the forces that act on the particle. The equation for the Hamiltonian is as follows:
![]() where
where
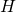 is the Hamiltonian
is the Hamiltonian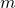 is particle mass
is particle mass is velocity = displacement per unit time
is velocity = displacement per unit time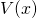 is the value of the potential energy at
is the value of the potential energy at 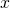
The term ![]() comes from Lagrangian mechanics. It relates to the path taken by a particle by one point in space to another. Specifically,
comes from Lagrangian mechanics. It relates to the path taken by a particle by one point in space to another. Specifically,
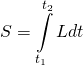 where
where
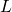 is called the Lagrangian. For a particle moving through a potential field, it equals the kinetic energy,
is called the Lagrangian. For a particle moving through a potential field, it equals the kinetic energy, 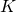 of the particle minus the potential energy,
of the particle minus the potential energy, 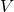 :
: 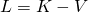 .
.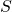 is a functional (a function of a function) called the action. The functions that comprise it are all of the possible paths between two points in space over the time interval
is a functional (a function of a function) called the action. The functions that comprise it are all of the possible paths between two points in space over the time interval 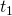 to
to 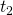 . The input to the functional is the integral noted above. The functional returns a number. That number can be plotted versus time.
. The input to the functional is the integral noted above. The functional returns a number. That number can be plotted versus time.- There is a single path that minimizes
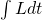
- We can find that minimum value of
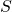 by setting its derivative to zero
by setting its derivative to zero
In the page on the Hamilton-Jacobi equation, it is shown that
(25) ![]()
where
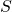 is the action
is the action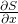 is the change of
is the change of 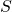 given a change in
given a change in 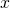
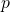 is the momentum (which equals mass x velocity,
is the momentum (which equals mass x velocity, 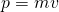 )
)
Note that the term for kinetic energy in the Hamiltonian, ![]() can be written
can be written ![]() . But we just said that
. But we just said that ![]() . Therefore,
. Therefore,
![]()
The term ![]() in the Hamiltonian remains unchanged.
in the Hamiltonian remains unchanged.
Given the above considerations, the classical form of the Hamilton-Jacobi equation becomes:
(26) ![]()
This equation describes the case where a particle is moving only in 1-dimensional space. If the particle is moving in 3-dimensional space, then, instead of taking the partial differential of ![]() only with respect to
only with respect to ![]() , we have to take the differential of
, we have to take the differential of ![]() in all three dimensions which we represent as
in all three dimensions which we represent as ![]() . This changes the above equation to:
. This changes the above equation to:
(27) ![]()
This bears a striking resemblance to the equation that Bohm derived:
(28) ![]()
The only difference between the two equations is the term to the far right. Bohm called this term the quantum potential, ![]() where
where
(29) ![]()
Bohm considered the quantum potential to be a real potential energy field that creates a force, the quantum force. In his scheme, classical potential fields create additional forces, and together, they determine how particles move through space. The classic potential field determines the classical behavior of a particle and the quantum potential determines the “quantum” behavior. In Bohm’s view, particles have definite positions and velocities at all times, and therefore, definite trajectories through space and time – positions and velocities and trajectories determined by the classical and quantum potential. And because the Schrodinger equation evolves deterministically, the trajectories of these particles are determined – from the beginning of time, actually. What makes these trajectories seem probabilistic to us stems from two facts. First, the positions and velocities of particles at the beginning of time are unknown to us. Since particle behavior follows the deterministic Schrodinger equation, if we didn’t know the position of the particles definitively at the beginning of time, then we’ll never know them. Second, when we make a measurement, we alter the trajectories in a manner that is unpredictable to us. Since, again, this makes the position and velocity of the particles unknowable to us at the time of measurement, we can’t predict where the determinant forces acting on them will make them end up in the future. Thus, to Bohm, it is not that particle behavior is inherently probabilistic, it’s just that, like in statistical mechanics, we don’t have enough detailed knowledge to make definite predictions.
Bohm considered the quantum potential to be a real potential energy field that creates a force, the quantum force. Classical potentials also create forces. These forces determine the positions, velocities and thus trajectories of particles. We know that classic forces produce a deterministic clockwork universe. The quantum potential produces quantum behavior which “appears” probabilistic. However, the Schrodinger equation evolves deterministically, and has evolved deterministically, since the beginning of time. In his original paper, Bohm states that there are two reasons that particle behavior appears probabilistic:
- 1) We don’t know the location of particles at the beginning of time, only a probability distribution of their locations (expressed as
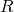 in the equation
in the equation 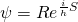 ). In contrast to the standard interpretation of quantum mechanics, it’s not that their location is intrinsically unknowable; it’s because we don’t have the ability to know their location. And because the wave function evolves deterministically according to the Schrodinger equation, we never will know the exact trajectory of particles – even though the particles follow a definite path.
). In contrast to the standard interpretation of quantum mechanics, it’s not that their location is intrinsically unknowable; it’s because we don’t have the ability to know their location. And because the wave function evolves deterministically according to the Schrodinger equation, we never will know the exact trajectory of particles – even though the particles follow a definite path. - 2) When we try to measure a particle, the measurement itself interacts with the particle and moves it in an unpredictable amount, adding additional indeterminacy to the measurement.
Bohm defines three conditions that must be present for the quantum potential to cause particles to behave in a way that is exactly the same as predicted by the standard interpretation of quantum mechanics:
- The
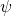 field satisfies Schrodinger’s equation.
field satisfies Schrodinger’s equation. - The particles momentum is restricted to
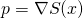 .
. - We are unable to know the location of a particle definitively, but instead, know the probability of finding the particle at a given location according to the equation
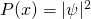
where
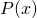 is the probability of finding the particle at position
is the probability of finding the particle at position 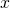
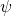 is the wave function of the particle
is the wave function of the particle
However, Bohm notes that if there were forces that act over a very short distance, over a very short time interval – and we were able to delineate these forces – then the above relationships for ![]() and
and ![]() might not hold and we might be able to determine the positions of particles definitively. If this were the case, then the uncertainty principle and all of the probabilistic behavior of particles that are part of the standard interpretation of quantum mechanics would no longer apply.
might not hold and we might be able to determine the positions of particles definitively. If this were the case, then the uncertainty principle and all of the probabilistic behavior of particles that are part of the standard interpretation of quantum mechanics would no longer apply.
Said more plainly, Bohm believed that there were so-called hidden variables at work – at time and distance scales much smaller than our experimental limits – that cause the quantum potential to have the values that it does and cause the probabilistic behavior that we observe.
Bohmian mechanics answers to questions raised by the Copenhagen interpretation
In so doing, Bohmian mechanics provides an alternative to the standard interpretation of quantum mechanics in explaining the conundrums outlined in the introductory section of this article. Let us enumerate them:
- The measurement problem – The standard interpretation of quantum mechanics says that quantum states – as given by wave functions – are indeterminate until measured, then mysteriously, these wave functions “collapse” upon measurement. In contrast, in Bohmian mechanics, particles have definite positions at all times. The information inherent in the wave function is present in the quantum potential. The quantum potential is associated with a quantum force that determines how particles move. The wave function in Bohmian mechanics is the wave function of the entire universe. It has evolved deterministically from the beginning of time and will continue to do so. It determines the movement of the particles whose positions are being measured in an experiment, the particles that make up the measuring device, the particles that make up an experimenter’s brain and the particles that make up everything else. A measurement is just an artificial grouping of particle movements that we define and give a special name. It’s no different than any other subset of particle movements. Thus, because there really is no such thing as a measurement, there is no such thing as wave function collapse. The wave function that is present after the group of particle movements that we arbitrarily define as a measurement is just a part of the deterministic evolution the wave function of the universe as it rolls on toward eternity.
- The double slit experiment – In Bohmian mechanics, the wave function – which is the wave function of the universe – determines the velocity of particles via the quantum potential. Therefore, it determines the trajectory of particles. And because the information content of the wave function in Bohmian mechanics is the same as the wave function in the standard interpretation of quantum mechanics, the patterns that Bohmian mechanics predicts will be made on the detector during the double slit experiment are the same as those predicted by the standard interpretation and those actually realized empirically. Given this model, Bohmian mechanics easily explains why individual photons shot at the detector when both slits are open create an interference pattern, if enough photons are delivered. The standard interpretation of quantum mechanics, on the other hand, has a difficult time explaining this.
Bohmian mechanics does a better job of explaining variants of the double slit experiment such as those described in the introduction to this article. For example, recall the variant double slit experiment in which a device is placed between one slit and the detector is activated or not activated only after a photon would have passed it. If the device is activated after the photon would have passed, then there is no interference pattern, jus as if the device had been activated before the photon could have passed. And if the device is left inactive after the photon would have passed, then there is an interference pattern, just as if the device had been left inactive before the photon could have passed. This is called retrograde causation. For the standard interpretation of quantum mechanics, this is just the way it is. However, the explanation in Bohmian mechanics is that the wave function of the universe drives the motion of particles – from the beginning of time, to the time of the “experiment” and for all times. Thus, that the experiment would be done, the set-up of the experiment and the experiment’s outcome – which are all just the groups of particle motions – would have all been determined from the beginning of time. Renowned physicist John Bell referred to this as superdeterminism. - Entanglement – The Bohmian mechanics explanation for entanglement is similar to the explanation for the double slit experiment and its variants. The wave function determines the quantum potential which determines particle motion, particle motion that includes the behavior of experiments involving entanglement. But the wave function is the wave function of the universe. Therefore, it is not surprising that the behavior of widely separated entangled particles can be affected simultaneously (i.e., the wave function is a non-local hidden variable).
Conclusion
This argument that was echoed several times in the last section seems to be the following: the wave function determines the quantum potential; the quantum potential determines particle movement; particle movement determines results of experiments and everything else; the wave function is predetermined at the beginning of time; therefore, the results of experiments and everything else is determined from the beginning of time. We just can’t ever predict what these results will be because we don’t have the technical capability of knowing the exact position of the particles of the universe – at the beginning of time or any other time – even though the particles do have an exact position at all times.
One might ask then: How does Bohm’s theory provide any better of a description of reality than the standard interpretation of quantum mechanics whose main edict is, that’s just the way it is?
In its initial iteration, it probably didn’t. However, Bohm strove to determine the nature of wave function throughout the remainder of his career, a crusade that culminated in his theory of the implicate and explicate order, a theory that is as much philosophy as it is science.
My novel, The Formula, offers speculation regarding the nature of the wave function as well. Without providing a spoiler, this speculation plays a central role in the theme of this novel. This paper, then, is meant to provide some explanation of the basis for this speculation, speculation that serves as an example of the considerable philosophical implications of Bohm’s theory.

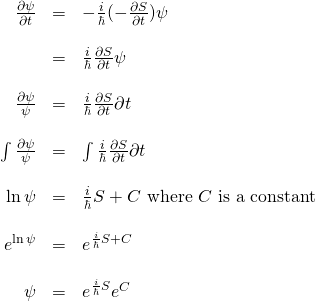
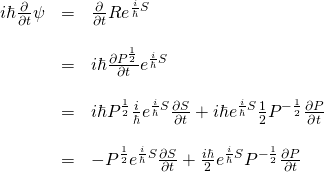
![Rendered by QuickLaTeX.com \begin{array}{rcl} -\frac{\hbar^2}{2m} \nabla^2 P^{\frac12} e^{\frac{i}{\hbar}S}&=&-\frac{\hbar^2}{2m} \nabla \left[ \nabla P^{\frac12} e^{\frac{i}{\hbar}S} \right]\\ &\,&\\ \nabla P^{\frac12} e^{\frac{i}{\hbar}S} &=& P^{\frac12} \frac{i}{\hbar} e^{\frac{i}{\hbar}S} \nabla S + e^{\frac{i}{\hbar}S} \frac12 P^{-\frac12} \nabla P \\ &\,&\\ \nabla(P^{\frac12} \frac{i}{\hbar} e^{\frac{i}{\hbar}S} \nabla S) &=& \left( \frac{i}{\hbar} P^{\frac12} \frac{i}{\hbar} e^{\frac{i}{\hbar}S} \nabla S + \frac{i}{\hbar} e^{\frac{i}{\hbar}S} \frac12 P^{-\frac12} \nabla P \right)\nabla S \,\, + \\ \,&\,& \frac{i}{\hbar} P^{\frac12} e^{\frac{i}{\hbar}S} \nabla^2 S \\ &\,&\\ &=& \frac{i^2}{\hbar^2} P^{\frac12} e^{\frac{i}{\hbar}S} (\nabla S)^2 + \frac{i}{2\hbar} e^{\frac{i}{\hbar}S} P^{-\frac12} \nabla P \nabla S \,\, + \\ \,&\,& \frac{i}{\hbar} P^{\frac12} e^{\frac{i}{\hbar}S} \nabla^2 S &\,&\\ \nabla \left( \frac12 e^{\frac{i}{\hbar}S} P^{-\frac12} \nabla P \right) &=& \left( (\frac12) e^{\frac{i}{\hbar}S} (-\frac12) P^{-\frac32} \nabla P + (\frac12) P^{-\frac12} (\frac{i}{\hbar}) e^{\frac{i}{\hbar}S} \nabla S \right)\nabla P \,\,+ \\ \,&\,& (\frac12) e^{\frac{i}{\hbar}S} P^{-\frac12} \nabla^2 P &\,&\\ &=& (-\frac14) e^{\frac{i}{\hbar}S} P^{-\frac32} (\nabla P)^2 + (\frac{i}{2\hbar}) P^{-\frac12} e^{\frac{i}{\hbar}S} \nabla S \nabla P \,\,+ \\ \,&\,& (\frac12) e^{\frac{i}{\hbar}S} P^{-\frac12} \nabla^2 P \end{array}](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-badaad1e08639ae8d94f2c6076999702_l3.png)