Trigonometric Identities

Contents

Figure 1

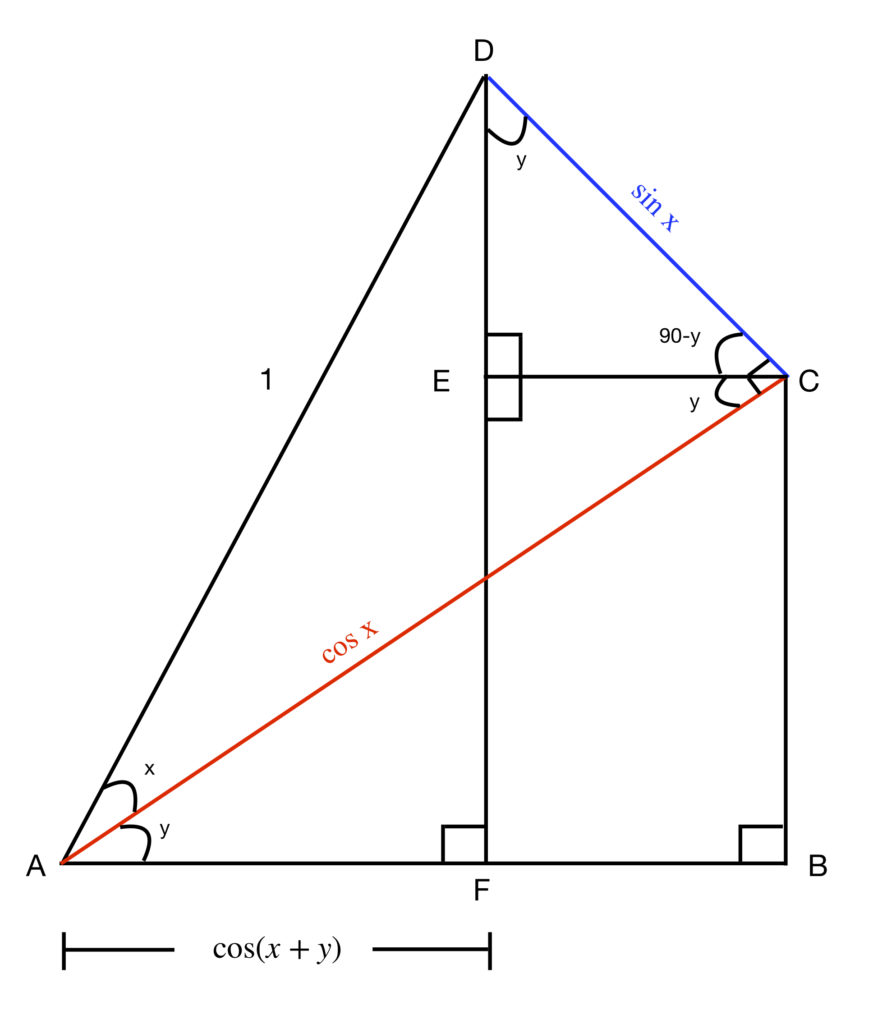
It may be useful to view the above diagram side-by-side with the following text. To do so, hold down the shift key and click on the figure. This will open the above figure in a new window. Once a new window is established, resize the current window and the new window with the figure in it so that both can be viewed simultaneously.

Sine two angle addition formula

We want to prove:

\sin(x+y)=\sin x \cos y+\cos x\sin y

Looking at figure 1, note that

  • \sin(x+y)=\overline{DF}
  • \overline{DF}=\overline{DE}+\overline{EF}
  • \overline{DE}
    • \cos y = \frac{\overline{DE}}{\sin x}\quad \text{therefore,}
    • \overline{DE}=\cos y \sin x
  • \overline{EF}
    • \overline{EF}=\overline{CB}
    • \overline{CB}=\sin y
    • \sin y = \frac{\overline{CB}}{\cos x}\quad \text{therefore,}
    • \overline{CB} = \cos x \sin y \text{; because}\,\overline{CB}=\overline{EF}
    • \overline{EF}=\cos x \sin y \text{;}
  • \text{substituting values of }\overline{DF}\text{,}\,\overline{DE}\,\text{and}\,\overline{EF}\text{, we are left with}
    • \sin(x+y)=\sin x \cos y+\cos x\sin y

Cosine two angle addition formula

We want to prove

\cos(x+y)=\cos x\cos y-\sin x \sin y

Looking at figure 1, note that

  • \cos(x+y)=\overline{AF}
  • \overline{AF}=\overline{AB}-\overline{FB}
  • \overline{AB}
    • \overline{AB}=\cos y
    • \cos y=\frac{\overline{AB}}\cos x\quad \text{therefore,}
    • \overline{AB}=\cos x \cos y
  • \overline{FB}
    • \overline{FB}=\overline{EC}
    • \overline{EC}=\sin y
    • \sin y = \frac{\overline{EC}}\sin x\quad \text{therefore,}
      • \overline{EC}=\sin x \sin y
    • \overline{EC}=\overline{FB}\quad \text{thus,}
    • \overline{FB}=\sin x \sin y
  • \text{substituting values of }\overline{AF}\text{,}\,\overline{AB}\,\text{and}\,\overline{FB}\text{, we are left with}
    • \cos(x+y)=\cos x\cos y-\sin x \sin y

Sine double angle formula

We want to prove

\sin 2x=2\sin x \cos x

From the sine two angle addition formula described above,

  • \sin(x+y)=\sin x \cos y+\cos x\sin y \quad \text{then,}
  • \sin(x+x)=\sin x \cos x+\cos x\sin x=2\sin x \cos x\quad \text{of course,}
  • \sin(x+x)=\sin 2x\quad \text{therefore,}
  • \sin 2x=2\sin x \cos x

Cosine double angle formula

We want to prove

\cos 2x = \cos^2x-\sin^2x

From the cosine two angle addition formula described above,

  • \cos(x+y)=\cos x\cos y-\sin x \sin y \quad \text{then,}
  • \cos(x+x)=\cos x\cos x - \sin x \sin x = \cos^2x-\sin^2x \quad \text{of course,}
  • \cos(x+x)=\cos 2x\quad \text{therefore,}
  • \cos 2x = \cos^2x-\sin^2x

Leave a Reply

Your email address will not be published. Required fields are marked *