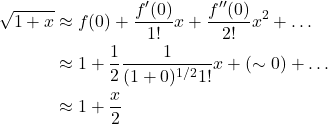This explanatory note largely follows the article of Fowler, Michael. “The Michelson-Morley Experiment.” U. Va. Physics, https://galileoandeinstein.phys.virginia.edu/lectures/michelson.html. I encourage the reader to check out this page and other pages by the author on special relativity as this site explains the basic concepts on which the subject hinges, in an easy-to-understand manner, as well as any resource I’ve come across.
At any rate, at the end of the nineteenth century, it was well known how sound propagated through various media. Thus, it was a reasonable assumption that light might behave in the same way. The media through which light was thought to propagate was referred to as the aether although it had never been found. The goal of the Michelson and Morley experiment, then, was to detect the aether. The ideas on which their experiment was based are outlined in figure 1.
Imagine 2 swimmers engaged in a race in a river with a current flowing with velocity v = 3 ft/sec, as shown. Both swim at the same speed: 5 ft/sec. The river is 100 ft wide. Swimmer A’s goal is to swim from point X to point Z and back. But recognizing that there’s a current, she knows that, to get from X to Z, she will need to swim at an angle towards point Y going to point Z and at the opposite angle going back. Swimmer B, on the other hand, starts at point Z, swims upstream 100 ft, then turns around and swims back to point Z. The question is, Who will win the race?
Well, we know that Swimmer B’s speed swimming upstream is c – v = 5 – 3 = 2 ft/sec and downstream is c + v = 5 + 3 = 8 ft/sec. Thus, the time it takes to swim upstream is 100 ft/2 ft/sec = 50 sec. The time it takes to swim downstream is 100 ft/8 ft/sec = 12.5 sec. Thus the total time for swimmer A is 62.5 sec.
As shown in figure 1A, the path for swimmer A forms a 3-4-5 triangle. Therefore, the speed at which swimmer A crosses the river is 4 ft/sec both going from points X to Z and from Z to Z. Swimmer A’s time for each leg of the race, then, is 100 ft/4 ft/sec = 25 sec. Swimmer A’s total time is, thus, 25 sec + 25 sec = 50 sec. So swimmer A wins.
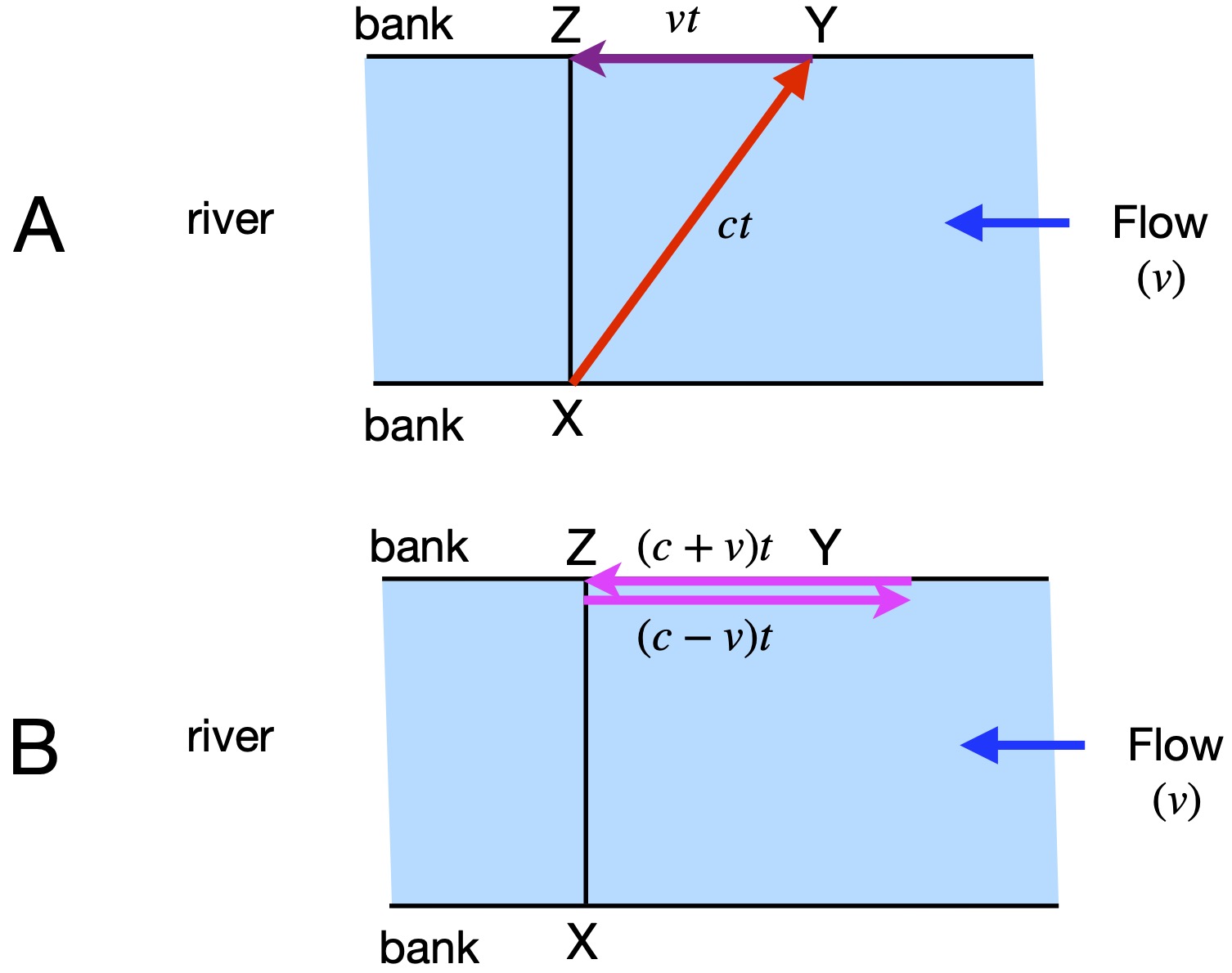
Michelson and Morley employed the same principles in their experiment. Figure 2 is a schematic of their experimental setup.
The aether is presumed to be flowing in the direction of the red arrows. Light is emitted from a source at s toward a (shown in green). At a, there’s a half-silvered, half-transparent mirror oriented at 45° which allows half of the light through toward c (depicted in yellow) and reflects the other half toward b (depicted in blue). At b there’s a mirror that reflects the light beam back toward a where it passes through the mirror to d. Likewise, at c, the light is reflected back to a, and at a, is reflected to d. At d, there’s a telescope that measures light intensity.
Just like the swimmers in the river, the light that follows the yellow path (i.e., the light moving across the “aether current” reaches d before the light following the blue path (which moves against, then with, the aether current).
Since the speed of light is incredibly fast and the flow of the aether was suspected to be quite slow (otherwise it would’ve already been found), it follows that the time delay that the experimenters would’ve had to detect would’ve been minuscule. It’s worth going through some calculations to see how minuscule.
We’ll need 2 approximation formulas to help with these calculations:
To see where these formulas come from, click .
For the blue path, the time traveling a distance ![]() from a to b is given by
from a to b is given by ![]() . The time traveling the same distance,
. The time traveling the same distance, ![]() , from b to a is
, from b to a is ![]() . The total time is:
. The total time is:
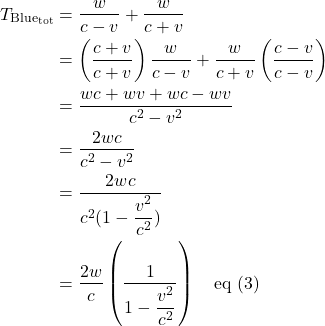
We assume ![]() so we use one of our estimation techniques:
so we use one of our estimation techniques:
We know that ![]() . Let
. Let ![]() . Then:
. Then:
![Rendered by QuickLaTeX.com \[ \frac{1}{1 - \displaystyle \frac{v^2}{c^2}} \approx 1 + \frac{v^2}{c^2} \]](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-3ccc268d7b79f7a2e75b5f882860779e_l3.png)
So:
![]()
Now for the yellow path. we know that the distance from a to c and back is ![]() . We find the speed of the yellow path in a fashion similar to that used for the swimmers:
. We find the speed of the yellow path in a fashion similar to that used for the swimmers:
Referring to figure 2, we see that d to a to c, then back to d forms a right triangle. It’s reproduced in figure 3.
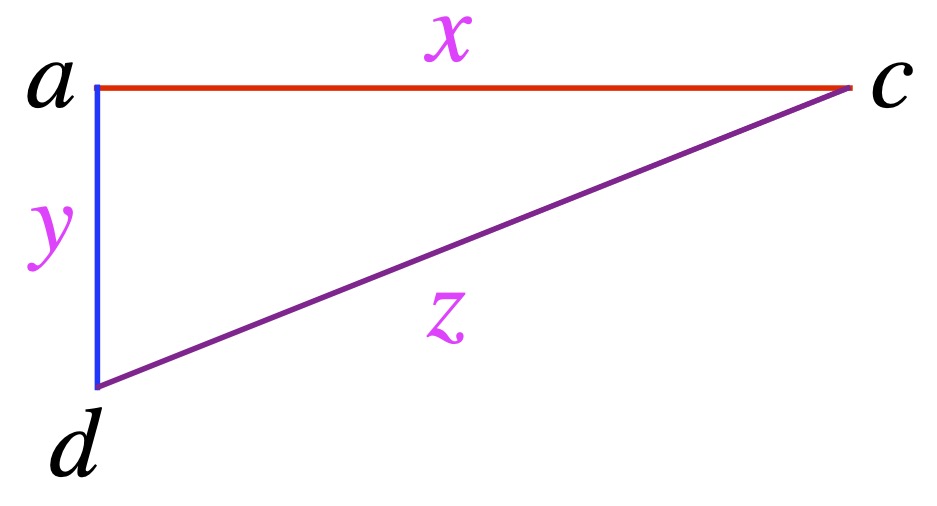
From the Pythagorean theorem, ![]() .
. ![]() is the speed of light (which we called
is the speed of light (which we called ![]() in describing the blue path).
in describing the blue path). ![]() is the quantity that we want to find.
is the quantity that we want to find. ![]() is the speed of the aether (which we called
is the speed of the aether (which we called ![]() previously). Thus:
previously). Thus:
![]()
Thus:
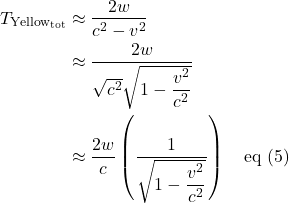
Again, because ![]() , we can use one of our estimates. Specifically:
, we can use one of our estimates. Specifically:
![]()
Let ![]() . Then we have:
. Then we have:
![]()
and
![Rendered by QuickLaTeX.com \[ T_{\text{Yellow}_{\text{tot}}} \approx \frac{2w}{c} \left(\frac{1}{1 - \displaystyle \frac{1v^2}{2c^2}}\right) \quad \text{eq (7)} \]](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-712692f7b80e6270d0f7f00c2b6cb0e0_l3.png)
Now we use the second approximation:
![]()
We let ![]() . Then:
. Then:
![Rendered by QuickLaTeX.com \[ $\displaystyle \frac{1}{1-\displaystyle \frac{1v^2}{2c^2}}} \approx 1+\displaystyle \frac{1v^2}{2c^2}}$ \]](https://www.samartigliere.com/wp-content/ql-cache/quicklatex.com-576d19795b92bb44d13e4c0d1e5cfb12_l3.png)
which means:
![]()
Comparing:
![]()
versus
![]()
We can see that the blue path takes ![]() longer than the yellow path.
longer than the yellow path.
![]() is the time it would take for light to make the round trip if there were no aether, perhaps a few millionths of a second. If we assume that the aether’s speed is about that of the earth’s orbit, then
is the time it would take for light to make the round trip if there were no aether, perhaps a few millionths of a second. If we assume that the aether’s speed is about that of the earth’s orbit, then ![]() and
and ![]() . This means the difference between the blue and yellow path should be about 1/100,000,000th of a few hundred millionths of a second. It seems that detecting this small a difference would be impossible. However, Michelson and Morley, found a way: by using the interference properties of the light waves as they traveled together from a to d.
. This means the difference between the blue and yellow path should be about 1/100,000,000th of a few hundred millionths of a second. It seems that detecting this small a difference would be impossible. However, Michelson and Morley, found a way: by using the interference properties of the light waves as they traveled together from a to d.
In their experiment, Michelson and Morley used light of a specific wavelength (i.e., color). If the light following the blue path arrived at a time such that it trailed the light following the yellow path by an even multiple of wavelength, then there should’ve been constructive interference. If it trailed the yellow path light by 1/2 wavelength, then there should’ve been destructive interference and the telescope should’ve detected no light. And if the light following the blue path trailed the light following the yellow path by some intervening distance, then the intensity of the light observed at d should be detectible but diminished, exhibiting an interference pattern.
The path length used by Michelson and Morley was 11 meters. Putting in some numbers, we can find the distance the blue path should trail the yellow light path:
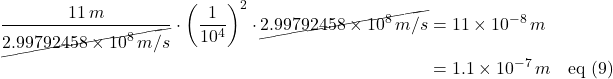
Michelson and Morley recognized that slight errors in mirror placement might produce such a lag. Therefore, they analyzed the interference pattern at one angle, rotated the apparatus 90° then measured the lag again. With the 90° change, the path of the light with respect to the purported aether flow should’ve switch positions. Thus, the phase shift after the 90° rotation should’ve been twice as large.
The wavelength of light used by Michelson and Morley was 500 nm (=5 x 10-7 m). Thus:
![]()
That means that the phase shift after the 90° rotation predicted by Michelson and Morley should have been about ![]() . What did they find? NOTHING. They repeated their experiment under other conditions (at different times of the year, on top of a mountain) but no significant phase shift was ever observed leading the authors to conclude that their was no aether flow (although Michelson is said to have been skeptical of his own findings.)
. What did they find? NOTHING. They repeated their experiment under other conditions (at different times of the year, on top of a mountain) but no significant phase shift was ever observed leading the authors to conclude that their was no aether flow (although Michelson is said to have been skeptical of his own findings.)
The Michelson-Morley result has often been called the greatest “failed” experiment in scientific history for it led scientists to believe that the aether did not exist and opened the door for special relativity (although Einstein claimed that he didn’t know about the Michelson-Morley experiment at the time that he developed special relativity.)
It’s worth noting that, shortly before the famous 1887 Michelson-Morley paper (in 1879), Michelson had provided the first accurate measurement of the speed of light. That result has been replicated (with improved accuracy) many times since and has never been refuted.