Poisson’s Equation – Sam Artigliere's Blog

I. Derivation

This derivation is patterned after that of Dr. Christian Salas.

It’s known in classical physics that the gravitational force is a conservative field that equals minus the gradient of the gravitational potential:

$\vec{F} = -\nabla \cdot \phi \quad \text{(1.1)}$

where

$\vec{F}$ is the gravitational force cause by a point mass, $M$
$\nabla = \displaystyle \frac{\partial}{\partial x}\hat{i} + \frac{\partial}{\partial y}\hat{j} + \frac{\partial}{\partial z}\hat{k}$
$\phi$ is the gravitational potential field, a scalar field

From Newton’s laws of gravitation, we have:

$\vec{F}(r) = -\frac{GM}{r^2}\hat{e}_r \quad \text{(1.2)}$

where

$\vec{F}(r)$ is the gravitational force at position $r$
$G$ is Newton’s gravitational constant
$M$ is the point mass that’s creating the gravitational force
$\hat{e}_r$ is a unit displacement vector in the radial direction

For a spherical surface, $S$ , of radius, $r$ , centered at a point mass, $M$ , located at the origin of our coordinate system, the total flux of the gravitational field, $\vec{F}$ , over the closed surface, $S$ , is given by the 3D flux theorem (proof):

$\begin{align*} \oint_S \vec{F} \cdot d\vec{S} &= \oint_S -\frac{GM}{r^2}\hat{e}_r \cdot d\vec{S} \\ &= -\frac{GM}{r^2} \oint_S \hat{e}_r \cdot \hat{e}_r \, dS \\ &= -\frac{GM}{r^2} \oint_S dS \\ &= -\frac{GM}{\cancel{r^2}} \cdot 4 \pi \cancel{r^2} \\ &= -G4\pi M \quad \text{(1.3)} \end{align*}$

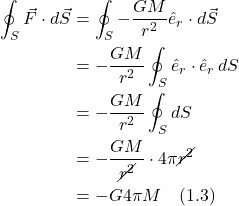
By the 3D divergence theorem (proof):

$\underset{S}{\int \int } \vec{F}\cdot d\vec{S} = \underset{V}{\int \int \int} \nabla \cdot \vec{F}\,dV \quad \text{(1.4)}$

where $V$ is the volume of the sphere enclosed by the spherical surface, $S$ . We also have:

$M=\underset{V}{\int \int \int} \rho\, dV \quad \text{(1.5)}$

where $\rho$ is the mass density (mass per unit volume) at each point. Then:

$\begin{align*} \oint_S \vec{F} \cdot d\vec{S} &= -G4\pi M \\ &= -G4\pi \underset{V}{\int \int \int} \rho\, dV \\ \underset{V}{\int \int \int} \nabla \cdot \vec{F}\,dV &= -G4\pi \underset{V}{\int \int \int} \rho\, dV \quad \text{(1.6)} \end{align*}$

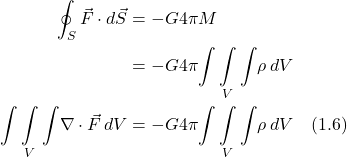
which means that:

$\nabla \cdot \vec{F} = -G4\pi \rho \quad \text{(1.7)}$

But, from eq. (1.1), $\vec{F} = -\nabla \cdot \phi$ . Thus:

$\begin{align*} \nabla \cdot \vec{F} &= -G4\pi \rho \\ \nabla\,(-\nabla \cdot \phi ) &= -G4\pi \rho \\ \nabla^2\,\phi &= G4\pi \rho \quad \text{(1.8)} \end{align*}$

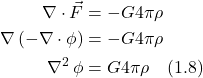
II. Solution

To solve Poisson’s equation, we use Green’s function. You can find more detailed information on Green’s function elsewhere on this site which you can access by clicking on this link. The general form of Poisson’s equation is:

$\frac{d^2 \phi(\vec{r})}{d\vec{r}^{\,\,2}} = g(\vec{r}) \quad \text{(2.1)}$

where

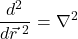$\displaystyle \frac{d^2}{d\vec{r}^{\,\,2}}=\nabla^2$ is the Laplacian operator
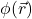$\phi(\vec{r})$ is a vector field that depends on position, 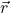$\vec{r}$ ; the electric and gravitational fields are the classic examples
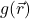$g(\vec{r})$ is the general result of the action of the Laplacian on 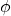$\phi$ . For gravitation, it’s $4\pi G \rho(\vec{r})$ .

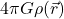(Note that Poisson’s equation is also applicable to electromagnetism where $g(\vec{r}) = \displaystyle \frac{\rho(\vec{r})}{\epsilon_0}$ , $\rho(\vec{r})$ representing charge density and $\epsilon_0$ is the permittivity of free space, a constant.)

To obtain the solution of Poisson’s equation using Green’s function, we start with:

$\phi(\vec{r}) = \int d^3 r^{\prime}\,G(\vec{r},\vec{r^{\prime}})\,g(\vec{r^{\prime}}) + \cancel{\, (c.f.)} \quad \text{(2.2)}$

where

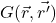$G(\vec{r},\vec{r^{\prime}})$ is the Green’s function
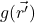$g(\vec{r^{\prime}})$ is the function which, when combined with the Green’s function, gives results at each point in space; these results are summed by the integral to yield the final solution
c.f. are the complementary solutions (solutions to the homogenous version of the equation); they’re crossed out because we’re not interested in them here

As a brief review, the Green’s function is analogous to an inverse matrix. Just as we multiply both sides of a matrix equation to get the solution, so multiplying both sides of the Poisson equation by Green’s function leads to the solution. Specifically:

$\nabla^2 G(\vec{r},\vec{r^{\prime}}) = \delta(\vec{r}-\vec{r^{\prime}})$

where $\delta(\vec{r}-\vec{r^{\prime}})$ is the Dirac delta function, a function that’s equal to 1 when $\vec{r}=\vec{r^{\prime}}$ but is 0 everywhere else.

Hence:

$\underbrace{\nabla^2 G(\vec{r},\vec{r^{\prime}})}_{1}\phi(\vec{r}) = \int d^3 r^{\prime}\,\underbrace{\nabla^2G(\vec{r},\vec{r^{\prime}})}_{1}\,g(\vec{r^{\prime}}) + \cancel{\, (c.f.)} \quad \text{(2.3)}$

In this manner, the Green’s function essentially “picks out” values of $g(r)$ at each position $r^{\prime}$ . Each of these values are then added up (as indicated by the integral sign) to give the total solution, $\phi(\vec{r})$ .

The key to solving our equation is finding the value of Green’s function. Once found, we substitute it back into eq. (2) and obtain the solution. To find the Green’s function, we need boundary conditions. For Poisson’s equation, the main boundary condition is that, as $\vec{r}\rightarrow \infty$ , $\phi(\vec{r})\rightarrow 0$ . This makes sense, since the farther away a mass gets from another mass, the weaker their gravitational attraction becomes. (The same is true for charges with opposite signs.)

To begin our quest to find Green’s function, we’ll make a simplification. We’ll let $\vec{R}=\vec{r}-\vec{r^{\prime}}$ . So the equation we have to solve is:

$\nabla^2_R G(\vec{R}) = \delta^3(\vec{R}) \quad \text{(2.4)}$

To do this, we should do something that will convert $\nabla^2$ into multiplication: namely, take the Fourier transformation. So:

$G(\vec{R})=\displaystyle \frac{1}{(2\pi)^3}\int d^3 k \,\displaystyle e^{i\vec{k} \cdot \vec{R}}\,\widetilde{G}(\vec{k}) \quad \text{(2.5)}$

The inverse Fourier transform is:

$\widetilde{G}(\vec{k}) = \int d^3 r\, \displaystyle e^{i\vec{k} \cdot \vec{R}}\,{G}(\vec{k}) \quad \text{(2.6)}$

We then substitute eq. (2.5) into eq. (2.4). Recall that $\nabla^2_R=\displaystyle \frac{d^2}{d\vec{R}^2}$ . It effects only the exponential term:

$\displaystyle \frac{\partial \,(e^{i\vec{k} \cdot \vec{R}})}{d\vec{R}}=i\vec{k}\,e^{i\vec{k} \cdot \vec{R}}$

$\displaystyle \frac{\partial^2(e^{i\vec{k} \cdot \vec{R}}) }{d\vec{R}^2} = \displaystyle \frac{\partial i\vec{k}\,(e^{i\vec{k} \cdot \vec{R}})}{d\vec{R}}=i^2\vec{k}\cdot\vec{k}\,e^{i\vec{k} \cdot \vec{R}}$

$=-k^2\,e^{i\vec{k} \cdot \vec{R}} \quad \text{(2.7)}$

Therefore, when we apply the Laplacian operator to $G(\vec{R})$ , we get:

$\nabla^2_R G(\vec{R}) = \displaystyle \frac{1}{(2\pi)^3} \,\int d^3 r\, \displaystyle e^{i\vec{k} \cdot \vec{R}}\,[-k^2\,\widetilde{G}(\vec{k})] = \displaystyle \frac{1}{(2\pi)^3} \,\int d^3 r\, \displaystyle e^{i\vec{k} \cdot \vec{R}}\quad \text{(2.8)}$

(Note that, since we took the Fourier transform of the lefthand side of eq. (2.4), we had to take the Fourier transform of the righthand side as well.)

Since $\displaystyle \frac{1}{(2\pi)^3} \,\int d^3 r\, \displaystyle e^{i\vec{k} \cdot \vec{R}} = \displaystyle \frac{1}{(2\pi)^3} \,\int d^3 r\, \displaystyle e^{i\vec{k} \cdot \vec{R}}$ , that means that:

$-k^2\,\widetilde{G}(\vec{k}) = 1 \quad \Rightarrow \quad \widetilde{G}(\vec{k}) = \displaystyle -\frac{1}{k^2} \quad \text{(2.9)}$

Putting the value of $\widetilde{G}(\vec{k})$ from eq. (2.9) into eq. (2.5) gives us:

$G(\vec{R})=\displaystyle -\frac{1}{(2\pi)^3}\int d^3 k \,\displaystyle \frac{e^{i\vec{k} \cdot \vec{R}}}{k^2} \quad \text{(2.10)}$

Solving the integral in eq. (10) will give us the Green’s function. However, to do this, we have to relate the $R$ and $k$ vectors. Left as is, this relationship is complicated (i.e., we’d need to use the addition theorem for the Legendre function of order 1). To solve this problem, we use the fact that the integrand is a scalar $\vec{k}\cdot\vec{R}$ , which means that this quantity is invariant under coordinate rotations. Thus, to make things easier, we rotate our coordinate system such that $\vec{R}$ aligns with the $k_z$ axis. This simplifies the relationship between $\vec{R}$ and $\vec{k}$ to $\vec{k}\cdot\vec{R}=\lvert \lvert\vec{k}\rvert\rvert \, \lvert \lvert\vec{R}\rvert\rvert\, \cos \theta$ where theta is the angle between the 2 vectors.

To do the integral, we use spherical coordinates. The volume element for our k-space in spherical coordinates is:

$d^3 k = k^2\,dk\,\sin \theta \, d\theta \, d\phi \quad \text{(2.11)}$

(To see where this comes from, click here.)

Substituting this expression for $d^3k$ into eq. (2.10) gives us:

$G(\vec{R})=\displaystyle -\frac{1}{(2\pi)^3}\displaystyle \int_0^{\infty} \cancel{k^2} dk\,\int_0^{\pi} \sin \theta d\theta\,\displaystyle \frac{e^{ikR\cos\theta}}{\cancel{k^2}}\,\int_0^{2\pi}d\phi$
$=\displaystyle -\frac{1}{(2\pi)^3}\displaystyle \int_0^{\infty} dk\,\int_0^{\pi} \sin \theta d\theta\,\displaystyle e^{ikR\cos\theta}\,\int_0^{2\pi}d\phi \quad \text{(2.12)}$

We can do the righthand integral first:

$\int_0^{2\pi}d\phi=\eval{\phi}_0^{2\pi}=2\pi - 0 = 2\pi\quad \text{(2.13)}$

When we put this back into eq. (12), the constant factor \frac{1}{(2\pi)^3} is reduced to \frac{1}{(2\pi)^2}. We put this back into eq. (2.12) and get:

$G(\vec{R})=\displaystyle -\frac{1}{(2\pi)^2}\displaystyle \int_0^{\infty} dk\,\int_0^{\pi} \sin \theta d\theta\,\displaystyle e^{ikR\cos\theta} \quad \text{(2.14)}$

Next, we work on the (new) righthand integral. Let

$u=\cos \theta$
$du=-\sin \theta\, d\theta$

The integral $\displaystyle \int_0^{\pi} \sin \theta d\theta\,\displaystyle e^{ikR\cos\theta}$ becomes $\displaystyle -\int_{1}^{-1} du\,\displaystyle e^{ikRu}$ . (The limits of integration change because $\cos 0 =1$ and $\cos\pi = -1$ .) When we change the sign of an integral, its upper and lower limits switch position. Therefore, our integral ends up being:

$\displaystyle \int_{-1}^{1} du\,\displaystyle e^{ikRu}\quad \text{(2.15)}$

The antiderivative of $e^{ikRu}$ is $\displaystyle \frac{e^{ikRu}}{ikR}$ . Evaluation of the integral in eq. (2.15) yields:

$\eval{\displaystyle \frac{e^{ikRu}}{ikR}}_{-1}^1 = \displaystyle \frac{e^{ikR}-e^{-ikR}}{ikR}\quad \text{(2.16)}$

Let $x=kR$ . Then

$\displaystyle \frac{e^{ikR}-e^{-ikR}}{ikR}=\displaystyle \frac{e^{ix}-e^{-ix}}{i}\cdot\frac{1}{x}\quad \text{(2.17)}$

We know that:

$\sin x = \displaystyle \frac{e^{ix}-e^{-ix}}{2i}$
$2\sin x = \displaystyle \frac{e^{ix}-e^{-ix}}{i}$

So,

$\displaystyle \frac{e^{ikR}-e^{-ikR}}{ikR}=\displaystyle \frac{2\sin kR}{kR}\quad \text{(2.18)}$

We put this expression, eq. (2.18), back into eq. (2.14). This yields:

$G(\vec{R})=\displaystyle -\frac{1}{(2\pi)^2}\displaystyle \int_0^{\infty} dk \displaystyle \frac{2\sin kR}{kR}$
$= \displaystyle -\frac{1}{2\pi^2 R}\displaystyle \int_0^{\infty} dk \displaystyle \frac{\sin kR}{k}\quad \text{(2.19)}$

The integral, $\displaystyle \int_0^{\infty} dk \displaystyle \frac{\sin kR}{k}$ is called the Dirichlet integral. It evaluates to $\displaystyle \frac{\pi}{2}$ . (To see a proof, click here.) Substituting this into eq. (2.19) leaves us with:

$G(\vec{R})=-\displaystyle \frac{1}{2\pi^2 R} \cdot \frac{\pi}{2} = -\frac{1}{4\pi R} \quad \text{(2.20)}$

Finally, we put $G(\vec{r}-\vec{r^{\prime}})$ into eq. (2) to get $\phi(\vec{r})$ :

$\begin{align*} \phi(\vec{r}) &= \int d^3 r^{\prime}\,G(\vec{r},\vec{r^{\prime}})\,g(\vec{r^{\prime}}) \\ &= \displaystyle \int_0^{\infty} d^3 r^{\prime}\,\left[-\frac{1}{\cancel{4\pi} R}\right]\,\,\cancel{4\pi} G(\rho(r^{\prime}))\\ &= -\displaystyle \frac{G}{R}\,\displaystyle \int_0^{\infty} d^3 r^{\prime}\,\rho(r^{\prime})\\ &= -\displaystyle \frac{GM}{R} \quad \text{(2.21)} \end{align*}$

Of course, eq.(2.21) is the equation for the gravitational potential.