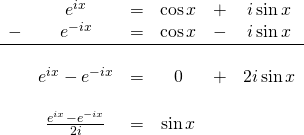Contents
Statement of Euler’s Formula
Euler’s formula is an extremely important formula that has many uses in mathematics and all of its applications. A statement of this formula is as follows:
![]()
Proof of Euler’s Formula
Using Taylor series
To prove Euler’s formula, we make use of the Taylor series expansions of ex, cosx, sinx and eix
![]()
![]()
![]()
![]()
Before we proceed, recall that ![]() . Therefore,
. Therefore,
Utilizing this information in our expression for ![]() :
:
![]()
Rearranging terms, we get
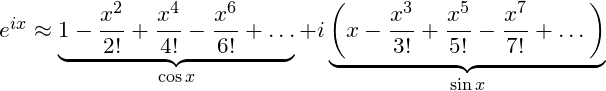
So
![]()
As discussed in the page on this site dealing with the Taylor’s Series, to prove that ![]() equals its Taylor series, we would have to prove that the error,
equals its Taylor series, we would have to prove that the error, ![]() , between
, between ![]() and its Taylor series goes to 0 as the number of terms in the Taylor series goes to infinity. Since the maximum value that the
and its Taylor series goes to 0 as the number of terms in the Taylor series goes to infinity. Since the maximum value that the ![]() derivative of
derivative of ![]() can take is 1, we have
can take is 1, we have

So
![]()
This is true for any value of ![]() we take the Taylor series around. Therefore,
we take the Taylor series around. Therefore, ![]() equals its Taylor series for all
equals its Taylor series for all ![]() .
.
Using derivative of Euler’s equation
Proof taken from http://math2.org/math/oddsends/complexity/e%5Eitheta.htm
If ![]() then the derivative of
then the derivative of ![]() is
is
![]()
Define a function, ![]() with the property that, just like
with the property that, just like ![]()
![]()
Now we solve this equation.
![]()
![]()
![]()
![]()
Let ![]() . We get
. We get
![]()
![]()
We need to see if there is any value of the constant, C_3, that makes ![]() . Set
. Set ![]() . We have
. We have
![]()
![]()
So ![]() when
when ![]() . Plug 1 into the equation for
. Plug 1 into the equation for ![]()
![]()
Corollaries
There are 2 important corollaries that can be derived directly from Euler’s formula. To prove these corollaries, we need 2 trigonometric identities:
A diagram that illustrates these identities can be found at the following site:
https://www.themathpage.com/aTrig/functions-angle.htm#theorem2
Cosine in terms of exponentials
Euler’s formula states:
![]()
Now substitute ![]() for
for ![]() . We get
. We get
![]()
Now add the 2 equations:
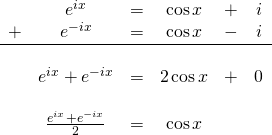
Sine in terms of exponentials
To prove this corollary, we perform subtraction on the 2 equations we added above: